Astronomy basics

Celestial sphere
- Equatorial coordinate system
Magnitude
Distances
- Parallax, $p$ or $\pi$
- Parsec, $pc$
Atmospheric effects
- Transparency and seeing
- Light pollution [1]

Celestial sphere

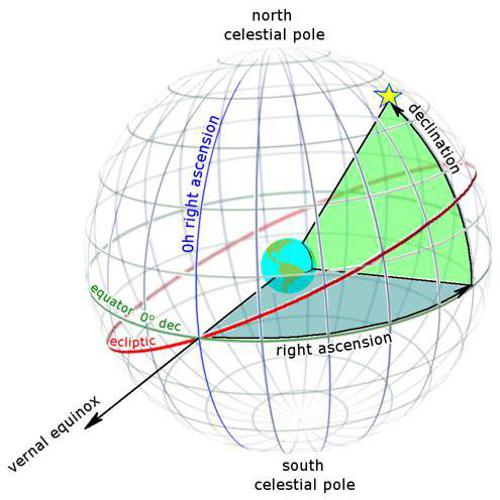
The celestial sphere is the geometrical space of all the points situated at the same distance from the Earth. Since the stars are very distant, they appear to occupy positions on the surface of this sphere.

We can plot the sun’s annual trajectory in the sky on it, the resulting line is called the ecliptic.

Equatorial coordinate system

Around the celestial sphere’s equator we measure Right Asension in hours (one hour = 15°). The intersection between the ecliptic, the celestial equator and the projection the Greenwhich meridian is called the vernal point, denoted by $\gamma$. $\gamma$ is considered to lie at RA 0^h, and going east RA increases by one hour for every 15° traveled.

Earth’s latitude circles are projected onto the celestial sphere and called Declination circles. We have 90° of positive DEC north of the Equator and 90° of negative DEC south of the Equator.

Note: stars with an angular DEC distance from the pole that’s lower than the observer absolute latitude are circumpolar, meaning they never rise or set.

Magnitude

In a clear night, without moonlight, with our naked eye we can see from 2500 to 3000 stars. About the same number are hidden away below the horizon. However there are infinitely more celestial bodies than these.

An object’s apparent brightness to a sensor is said to be its apparent magnitude. This is based on how the object is observed from Earth, meaning it depends on the distance, its luminosity and the extinction. The higher the value, the fainter an object is. Visual magnitude is usually denoted by $m$ or $m_v$.

The absolute magnitude ($M$) describes the intrinsic luminosity emitted by an object and is defined to be equal to the apparent magnitude that the object would have if it were placed at a certain distance from Earth, 10 parsecs for stars.

Distances

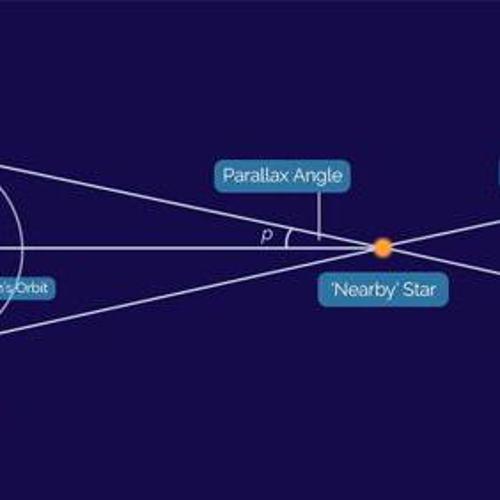
Parallax, $p$ or $\pi$

Parallax (from Ancient Greek παράλλαξις (parallaxis)), meaning ‘alternation’ is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. Due to foreshortening, nearby objects show a larger parallax than farther objects when observed from different positions, so parallax can be used to determine distances.

To measure large distances, such as the distance of a planet or a star from Earth, astronomers use the principle of parallax. Here, the term parallax is the semi-angle of inclination between two sight-lines to the star, as observed when Earth is on opposite sides of the Sun in its orbit.

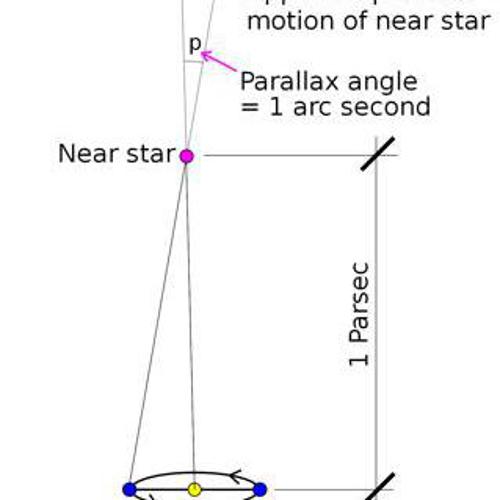
Parsec, $pc$

One parsec is the distance from Earth to a point whose parallax p = 1” (arcsecond).

For small angles, the distance to an object: $d_{(pc)}=\frac{1}{p_{(arcsecond)}}$.

$~1pc = 3.26ly$

Note: we can only measure parallaxes $p > 0.001” (~1000pc)$, because of atmospheric distortion.

Atmospheric effects

Transparency and seeing

Transparency defines the clarity of the atmosphere, and affects the quality of images obtained through a telescope and of astrophotos. It’s determined by your altitude, weather conditions, dust particles floating around etc.

It is measured on the Antoniadi scale:

I Perfect seeing without a quiver of turbulence at all.
II Slight shimmers; moments of stillness last several seconds.
III Average seeing; larger air tremors blur the view.
IV Poor views with a constant and disturbing swell.
V Bad views with severe undulations; so unstable that even quick sketches are out of the question.

Light pollution [1]

Light pollution is measured using the Bortle scale.

Class	Title	NELM	Approx. SQM¹ mag/arcsec²	Description	Color
1	Excellent dark-sky site	7.6–8.0	21.7–22.0	the zodiacal light is visible and colorful the gegenschein is visible the zodiacal band is visible airglow is readily visible the Scorpius and Sagittarius regions of the Milky Way cast obvious shadows many constellations, particularly fainter ones, are barely recognizable amid the large number of stars many Messier and globular clusters are naked-eye objects M33 is a direct vision naked-eye object limiting magnitude with reflector is 17.5 (with effort) Venus and Jupiter affect dark adaptation	Black
2	Typical truly dark site	7.1–7.5	21.5–21.7	the zodiacal light is distinctly yellowish and bright enough to cast shadows at dusk and dawn airglow may be weakly visible near horizon clouds are only visible as dark holes against the sky surroundings are barely visible silhouetted against the sky the summer Milky Way is highly structured many Messier objects and globular clusters are naked-eye objects M33 is easily seen with naked eye limiting magnitude with 12.5" reflector is 16.5	Gray
3	Rural sky	6.6–7.0	21.3–21.5	the zodiacal light is striking in spring and autumn, and color is still visible some light pollution evident at the horizon clouds are illuminated near the horizon, dark overhead nearer surroundings are vaguely visible the summer Milky Way still appears complex M15, M4, M5, and M22 are naked-eye objects M33 is easily visible with averted vision limiting magnitude with 12.5" reflector is 16	Blue
4	Rural/suburban transition	6.1–6.5	20.4–21.3	the zodiacal light is still visible, but does not extend halfway to the zenith at dusk or dawn light pollution domes visible in several directions clouds are illuminated in the directions of the light sources, dark overhead surroundings are clearly visible, even at a distance the Milky Way well above the horizon is still impressive, but lacks detail M33 is a difficult averted vision object, only visible when high in the sky limiting magnitude with 12.5" reflector is 15.5	Green/Yellow
5	Suburban sky	5.6–6.0	19.1–20.4	only hints of zodiacal light are seen on the best nights in autumn and spring light pollution is visible in most, if not all, directions clouds are noticeably brighter than the sky the Milky Way is very weak or invisible near the horizon, and looks washed out overhead when it is half moon (first/last quarter) in a dark location the sky appears like this, but with the difference that the sky appears dark blue limiting magnitude with 12.5" reflector is 15	Orange
6	Bright suburban sky	5.1–5.5	18.0–19.1	the zodiacal light is invisible light pollution makes the sky within 35° of the horizon glow grayish white clouds anywhere in the sky appear fairly bright even high clouds (cirrus) appear brighter than the sky background surroundings are easily visible the Milky Way is only visible near the zenith M33 is not visible, M31 is modestly apparent limiting magnitude with 12.5" reflector is 14.5	Red
7	Suburban/urban transition	4.6–5.0	18.0–19.1	light pollution makes the entire sky light gray strong light sources are evident in all directions clouds are brightly lit the Milky Way is nearly or totally invisible M31 and M44 may be glimpsed, but with no detail through a telescope, the brightest Messier objects are pale ghosts of their true selves when it is full moon in a dark location the sky appears like this, but with the difference that the sky appears blue limiting magnitude with 12.5" reflector is 14	Red
8	City sky	4.1–4.5	<18.0	the sky is light gray or orange – one can easily read stars forming familiar constellation patterns may be weak or invisible M31 and M44 are barely glimpsed by an experienced observer on good nights even with a telescope, only bright Messier objects can be detected limiting magnitude with 12.5" reflector is 13	White
9	Inner-city sky	4.0	<18.0	The sky is brilliantly lit many stars forming constellations are invisible and many fainter constellations are invisible aside from the Pleiades, no Messier object is visible to the naked eye the only objects to observe are the Moon, the planets, and a few of the brightest star clusters	White

Bortle Scale - Wikipedia